Mini Concours ENSA

La valeur de la limite est: $$\lim _{x \rightarrow 0} \frac{e^{3 x}-e^{2 x}}{\sin x}$$

On pose $$: I=\int_{0}^{\frac{\pi}{6}} \sin \theta \cos ^{2} \theta d \theta$$ et $$J=\int_{0}^{\frac{\pi}{6}} \sin ^{3} \theta d \theta$$

L’argument du nombre complexe $$z$$ est égale à : $$Z=\frac{(1+i)^{21}(1+i \sqrt{3})^{19}}{(1-i)^{9}}$$

L’intégrale $$\int_{1}^{e} \frac{1}{x(1+\ln x)} d x$$ est égale à :

Le domaine de définition de la fonction $$\mathrm{f}$$ est:
$$f(x)=\frac{\ln \left(4-x^{2}\right)}{\ln (x+1)}$$

La limite de la suite $$\sum_{k=1}^{n} \frac{n}{n^{2}+k}$$ est égale à :

La valeur de $$\int_{0}^{\pi} \sin (3 x) \cos (2 x) d x$$ est :

Si $$\theta$$ est un nombre réel alors $$(\cos \theta)^{4}$$ est égale à :

L’ensemble de solution de l’inéquation $$x \ln (x+1)>0$$ est:

La valeur de $$\int_{-1}^{0} \frac{1}{2 x^{2}-3 x+1} d x$$ est :

Depuis un point $$\mathrm{O}$$ , on lance vers le haut avec une vitesse initiale $$\vec{v}_{0}$$ , suivant la ligne de plus grande pente d’un plan incliné d’angle $$\alpha$$ par rapport à l’horizontale, un solide de masse $$\mathrm{m}$$ . il s’arrête après avoir parcouru une distance $$L$$ , puis redescend.

Tout au long de son mouvement il est soumis à une force de frottement $$\vec{f}, \mathrm{~d}$$ ‘intensité constante.
On donne : $$\mathrm{m}=200 \mathrm{~g} ; \sin \alpha=0,1 ; v_{0}=3 \mathrm{~m} \cdot \mathrm{s}^{-1} ; \mathrm{g}=10 \mathrm{~m} \cdot \mathrm{s}^{-2} ; f=0,1 \mathrm{~N}$$ .
Parmi les propositions suivantes une seule est exacte.

Lors d’une mission humanitaire, un avion des Nations Unies, volant horizontalement à l’altitude
$$\mathrm{z}=3,0.10^{3} \mathrm{~m}$$ , à vitesse constante $$v_{0}$$ , largue, en un point $$\mathrm{S}$$ , un colis de vivres. La résistance de l’air est considérée comme négligeable devant les autres forces s’exerçant sur le colis.
Données : accélération de la pesanteur $$g=10 \mathrm{~m} \cdot \mathrm{s}^{-2} ; \sqrt{6}=2,4 ; \sqrt{3}=1,7$$ .
Choisir la ou les bonnes réponses

Une benne transporte un objet de masse $$m$$ positionné comme indiqué sur la figure cidessous. La benne se soulève à vitesse constante et au bout de 30 secondes, l’objet se met à glisser et le chauffeur arrête immédiatement la benne. L’angle entre le plancher de la benne et l’horizontale est alors $$\theta=30^{\circ}$$ .
Données : $$\sin 30^{\circ}=0,5 ; \cos 30^{\circ}=0,8 ;$$ tang $$30^{\circ}=0,5 ; \mathrm{g}=10 \mathrm{~m} \cdot \mathrm{s}^{-2}$$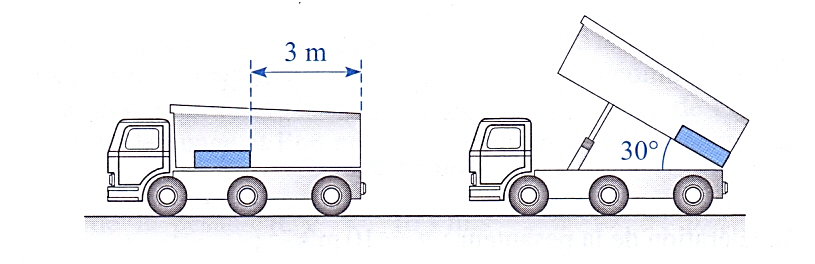

La force de frottement statique, quand elle est maximale, a pour expression $$f_{\max }=\mu R, \mathrm{R}$$ étant la réaction entre le plancher la benne.

On considère la Terre de masse $$\mathrm{M}_{\mathrm{T}}$$ , de rayon $$\mathrm{R}$$ et un objet de masse $$\mathrm{m}$$ . L’objet gravite autour de la Terre et est situé à une distance $$\mathrm{h}$$ de sa surface. On néglige dans tout cet exercice les frottements dus à la résistance de l’air et on prendra la constante de gravitation $$G=6 ; 7.10^{-11}$$ (SI), l’accélération de la pesanteur, notée $$\mathrm{g}$$ , comme étant uniforme et égale à $$10 \mathrm{~m} \cdot \mathrm{s}^{-2}$$ et le rayon de la Terre $$\mathrm{R}_{\mathrm{T}}=6700 \mathrm{~km}$$ .

On considère un pendule simple constitué d’une masse m ponctuelle accroché au bout d’une tige rigide de masse négligeable et de longueur L. cette tige est articulée autour d’un point fixe $$\mathrm{O}$$ et peut se mouvoir dans un plan vertical. On repère la position du pendule par l’angle $$\theta$$ qu’il fait avec la verticale. L’origine des énergies potentielles est- prise quand $$\theta=0$$ . Dans l’état initiale, le pendule est lancé avec les conditions suivante :
$$\theta_{0}=0$$ et $$\left[\frac{d \theta}{d t}\right](0)=\alpha \sqrt{\frac{g}{L}} \alpha$$ étant une constante. On suppose que le mouvement se fait sans frottement.